『くもわ』の法則 – 小学算数《割合》の求め方にはこの『公式』が便利

中学受験に必要な算数に割合というのがあります。
割合の表し方はいくつかあり、小数、分数、百分率（%）、歩合（○割○分）で表されます。

この割合の公式がなるべく簡単に覚えられる方法を紹介します。

はじめに

一般的には「もとになる量」「くらべる量」「割合」という言葉を使いますがこの時点で少しわかりづらいですよね。

「もとになる量」と「くらべる量」がどっちのことを言っているのか？

これについては、あとで例題を見ながら理解していきましょう。

割合の求め方　公式

「割合」＝「くらべる量 ÷ 「もとになる量」

「くらべる量」＝「もとになる量」 × 「割合」

「もとになる量」＝「くらべる量」 ÷ 「割合」

これだけでは覚えるの大変です。

まずは簡単な例題を見て見ましょう。

例えばボールが全部で 100 個あります。その中にピンク色のボールが 30 個あります。
ピンク色のボールの割合はいくつですか？

もとになる量：全部のボールの数＝ 100 ＝全部の量

くらべる量　：ピンクのボールの数＝ 30 ＝割合を知りたい量

簡単なこの数ならピンクのボールが30％とわかりますよね。
100のうちの30だから30％。

「もとになる量」と「くらべる量」の関係がわかりましたか？
どういう風に計算するのでしょうか？

その前に下の図の小数、分数、百分率（%）、歩合の関係を見てみましょう。

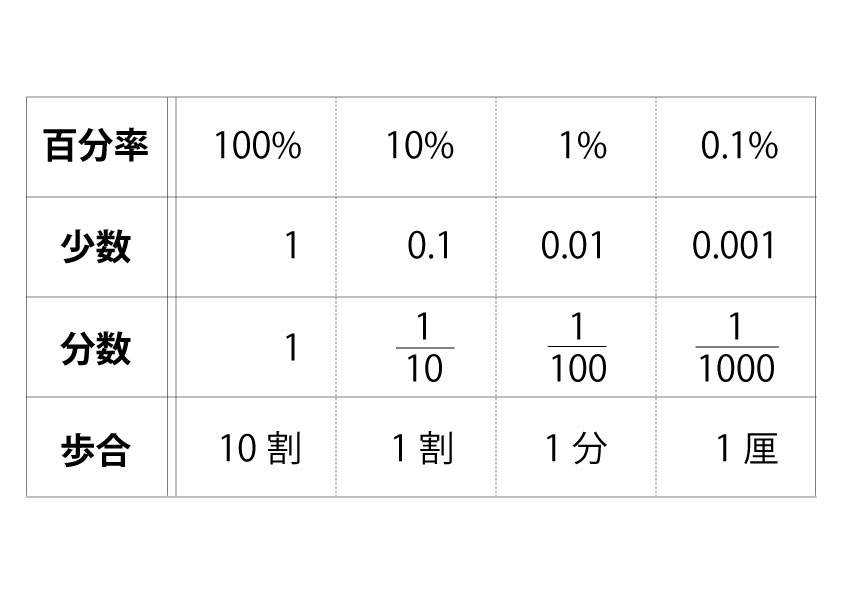
百分率は何％と表すことができます。これを表を見るとわかりやすいですね。
30％だと小数の場合は0.3になるのがわかります。

分数も簡単ですね。100個あるうちの30個なので 30/100(100が分母で30が分子)、約分すると 3/10(10が分母で3が分子)となります。

では、計算方法を紹介します。

「もとになる量」「くらべる量」「割合」の関係を公式にしたものをもう一度見てみます。

「割合」＝「くらべる量 ÷ 「もとになる量」

「くらべる量」＝「もとになる量」 × 「割合」

「もとになる量」＝「くらべる量」 ÷ 「割合」

覚えにくいですよね。

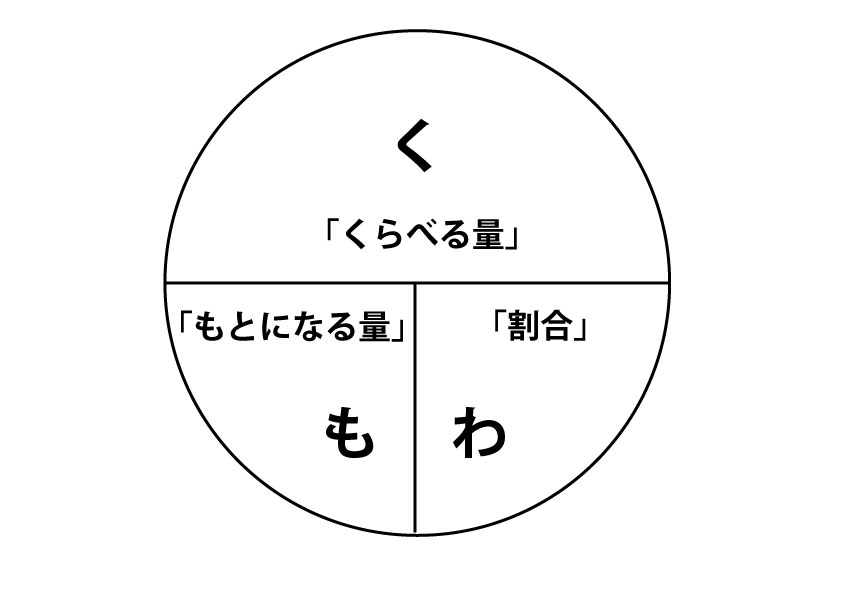
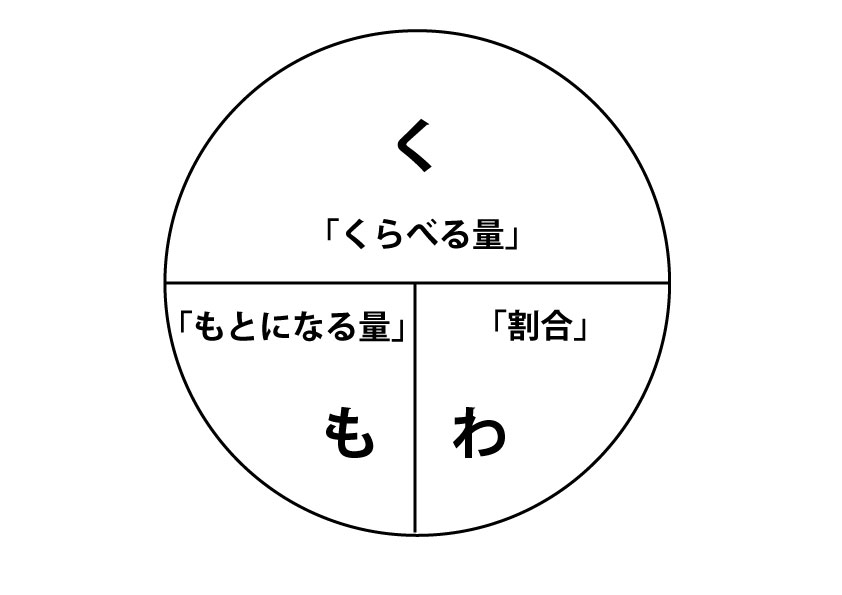
くもわの法則です。

さらにわかりやすくします。

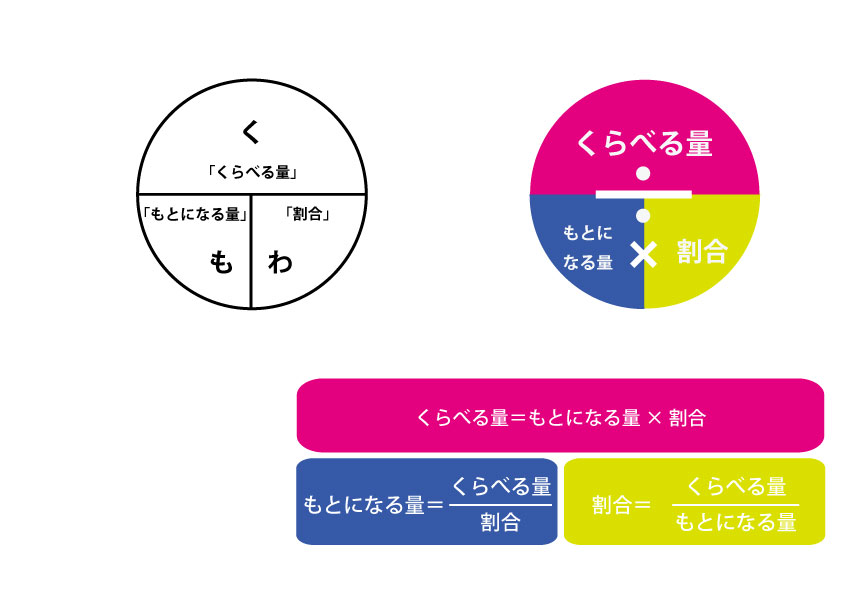
公式がずーっとわかりやすくなりました！

「割合」＝「くらべる量 ÷ 「もとになる量」

「くらべる量」＝「もとになる量」 × 「割合」

「もとになる量」＝「くらべる量」 ÷ 「割合」

印刷版もチェック！

《NEXT：問題を解いてみる＋要点まとめ》