苦手な人が多い滑車の問題の解き方をなるべく簡単に紹介していきます。
上の写真のようなものが滑車と言われるものです。物を上に移動させるときなどに使います。
ここで、テストに頻出する滑車問題の基礎をしっかり覚えて、応用問題に挑戦できるようにしましょう。
重要な基本原理
滑車のすべての問題は、2つの原理を理解していれば簡単に解けるようになります。
原理1:1本の糸にはたらく力の大きさはすべて等しい。
原理2:上に引っ張る力の和と下に引っ張る力の和はつねに等しい。
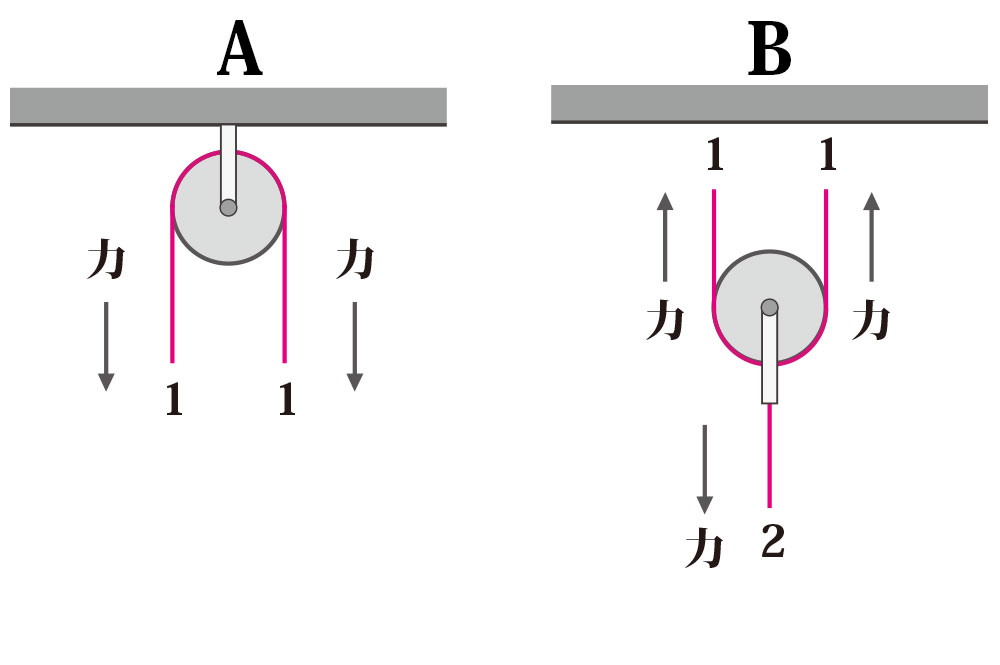
図A:1本の糸にはたらく力の大きさはすべて等しい。
図B:上に引っ張る力の和と下に引っ張る力の和はつねに等しい。
図の A は、天井に固定された定滑車と言われているものです。
図の B は、固定されていない動滑車と言われているものです。
重要なポイント
1. 定滑車で糸を引き上げる『きょり』とおもりが移動する『きょり』が等しい。
2. 定滑車で糸を引く『ちから』おもりのおもさは等しい。
3. 動滑車で糸を引き上げる『きょり』は、おもりが移動する『きょり』の 2倍。
4. 動滑車はおもりの 半分(1/2)の『ちから』で糸をひくことができる。
言葉だけではわかりづらいので、図と問題で説明していきます。
定滑車の問題
1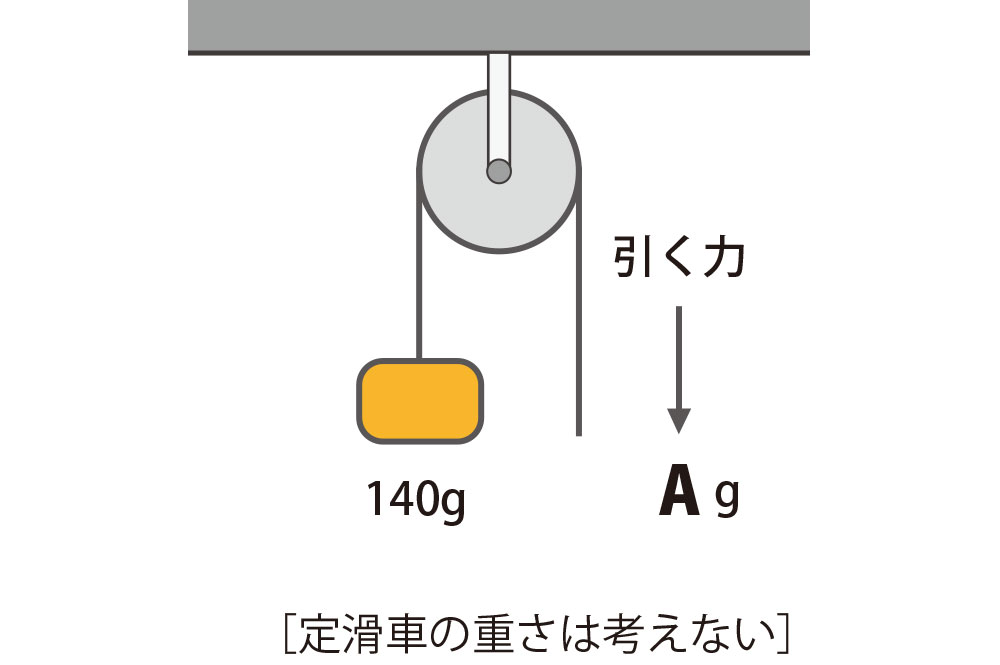
Aは何グラムでしょう? 滑車の重さは考えないでください。
1本の糸にはたらく力の大きさはすべて等しい ので、
A = 140g
となります。
2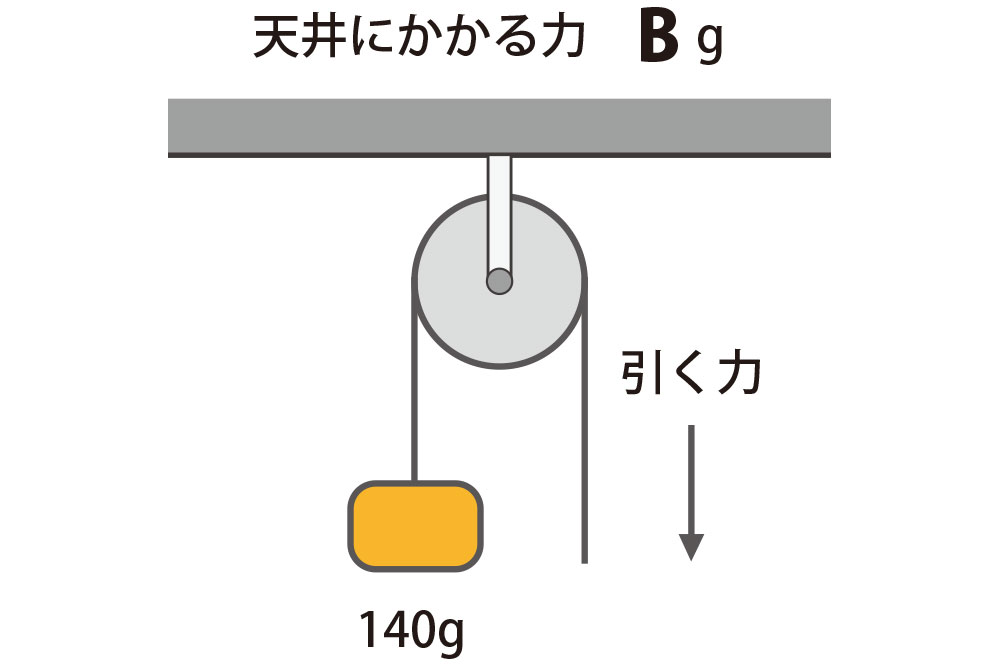
天井にかかる力 B は何グラムでしょう?滑車の重さは考えないでください。
1本の糸にはたらく力の大きさはすべて等しい ので、両方の糸に140グラムのちからがかかります。
B = 280g
となります。
3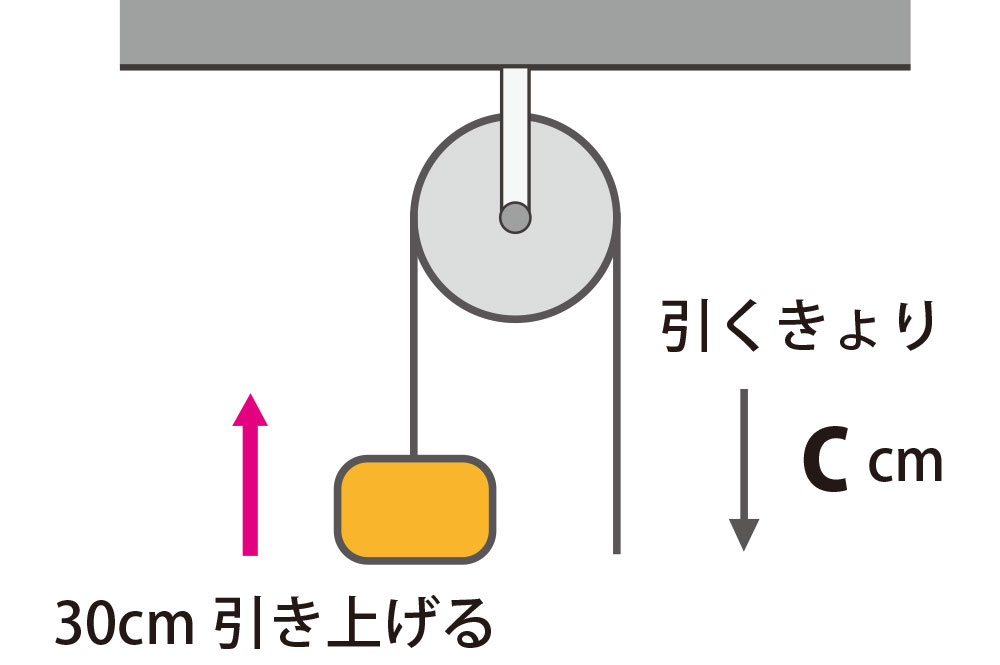
C は何cm 移動するでしょうか?
定滑車で糸を引き上げる『きょり』とおもりが移動する『きょり』が等しい ので
C = 30 cm
となります。
4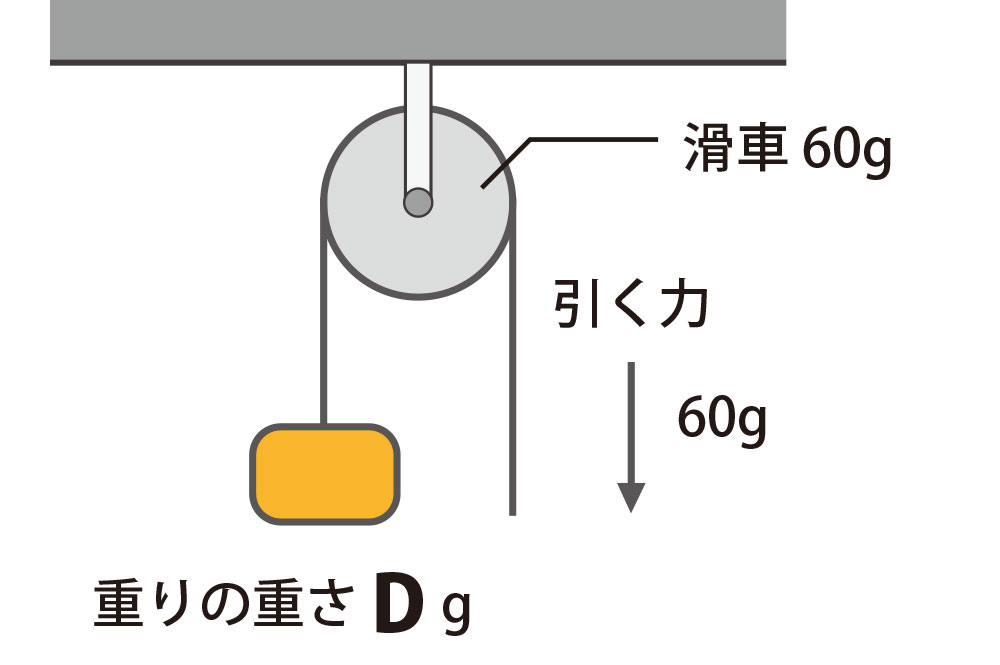
D は何グラムでしょうか?
1本の糸にはたらく力の大きさはすべて等しい ので、
D = 60g
となります。
5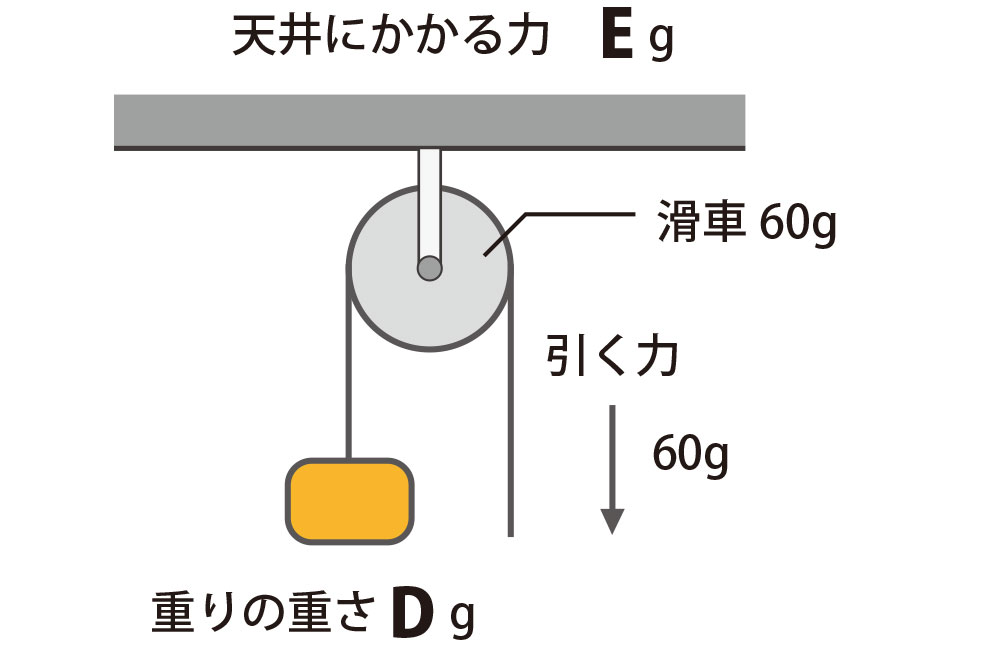
天井にかかる重さ E は何グラムでしょうか?
1本の糸にはたらく力の大きさはすべて等しい ということと、さらに滑車の重さが含まれます。
60 + 60 + 60 = E
E = 180g
となります。
動滑車の問題
1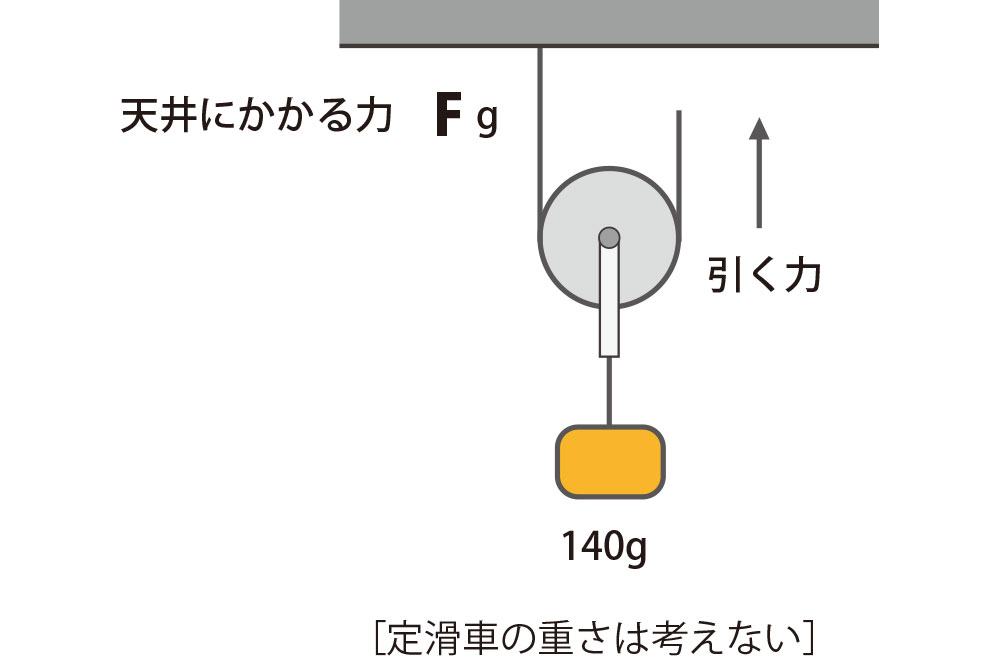
天井にかかる重さFは何グラムでしょうか?
上に引っ張る力の和と下に引っ張る力の和はつねに等しいなので
上に引っ張る力=糸2本
下に引っ張る力=糸1本・おもり140g
糸2本 = 140g → 糸1本 ( F )=70g
F = 70g
となります。
2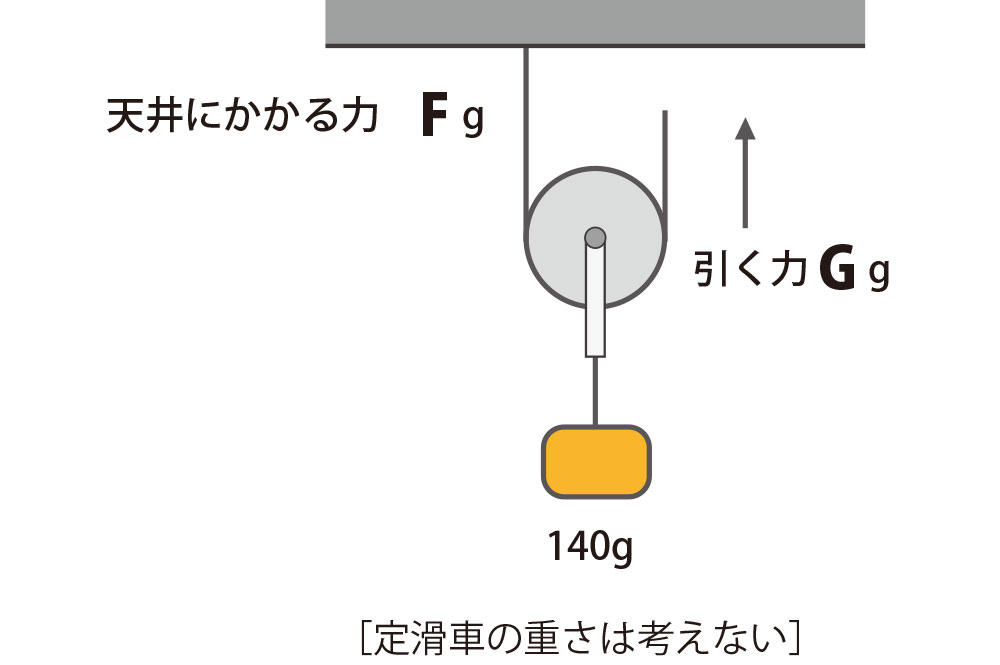
引く力Gは何グラムでしょうか?
上に引っ張る力の和と下に引っ張る力の和はつねに等しいなので
上に引っ張る力=糸2本
下に引っ張る力=糸1本・おもり140g
糸2本 = 140g → 糸1本 =70g
G = 70g
となります。
3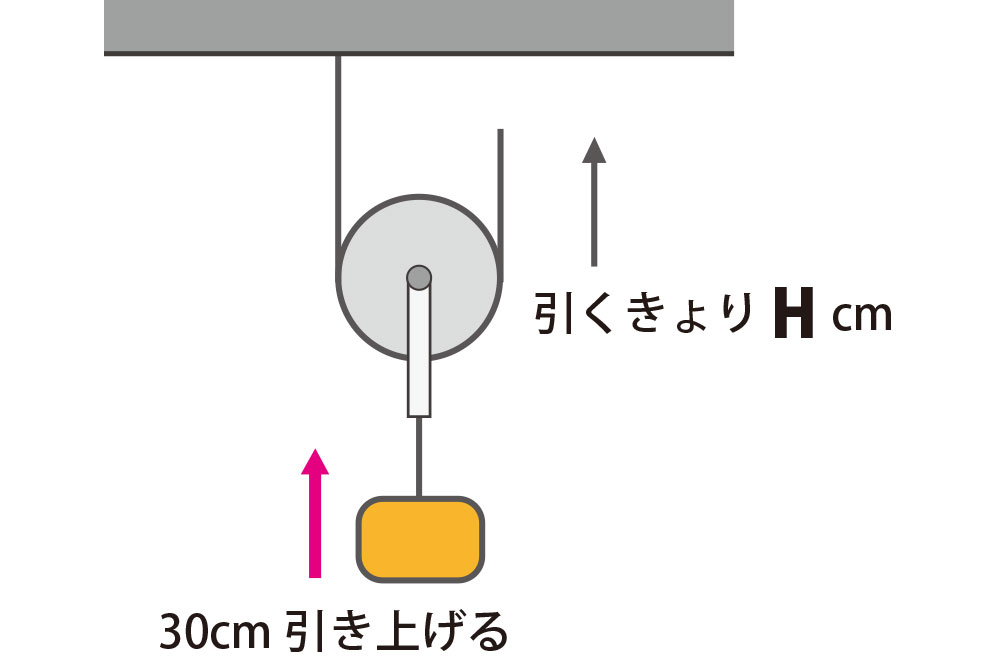
引くきょり H は何cm でしょうか?
動滑車で糸を引き上げる『きょり』は、おもりが移動する『きょり』の 2倍 なので
30cm x 2 = H
H = 60cm
となります。
4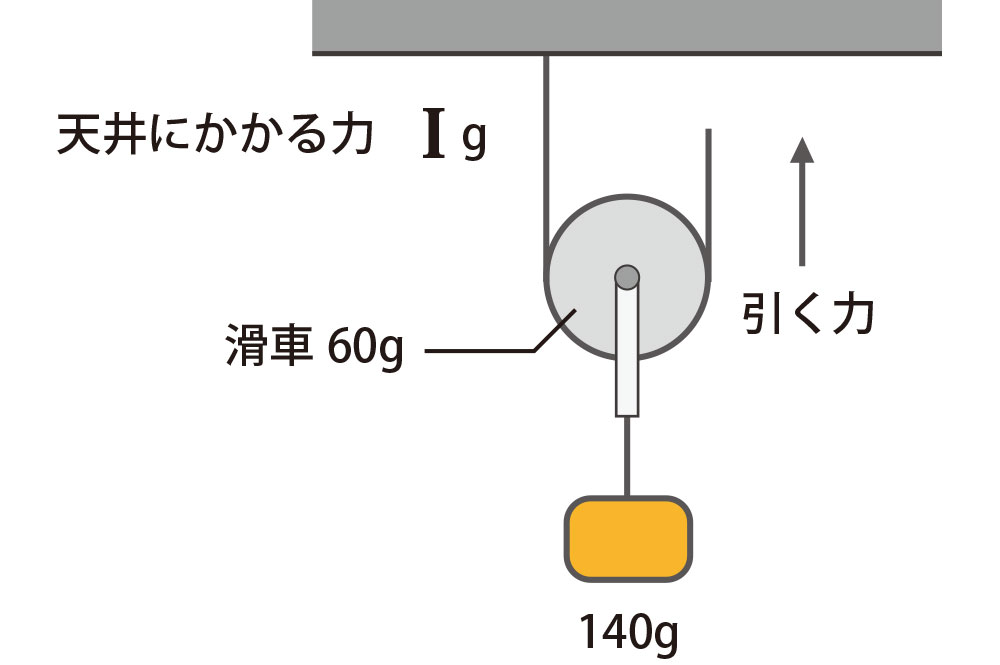
I の天井にかかるちからは何グラムでしょうか?
滑車の重さが含まれるので注意しましょう。
上に引っ張る力の和と下に引っ張る力の和はつねに等しい。
動滑車はおもりの 半分(1/2)の『ちから』で糸をひくことができる。
これらのことから、
(60 + 140)÷ 2 = I
I = 100g
となります。
5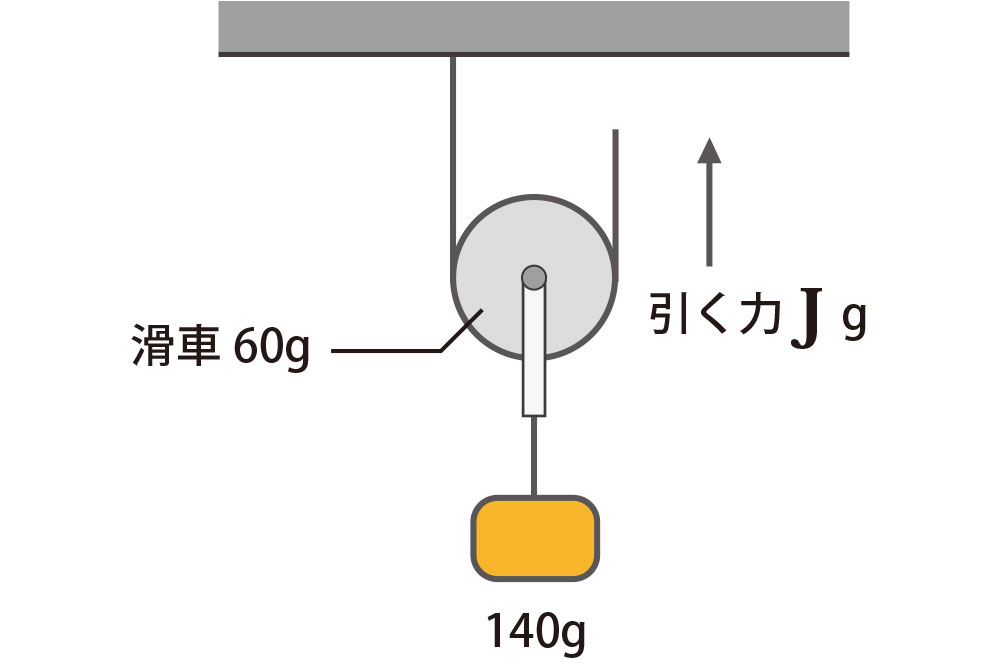
引くちから J は何グラムでしょうか?
滑車の重さが含まれるので注意しましょう。
上に引っ張る力の和と下に引っ張る力の和はつねに等しい。
動滑車はおもりの 半分(1/2)の『ちから』で糸をひくことができる。
これらのことから、
(60 + 140)÷ 2 = J
J = 100g
となります。
以上、『定滑車』『動滑車』の問題の解き方をなるべくシンプルにまとめました。
覚えることは6つです。基本を覚えれば応用問題にも対応できるのでしっかり覚えましょう。
覚えること6つ
1. 1本の糸にはたらく力の大きさはすべて等しい。
2. 上に引っ張る力の和と下に引っ張る力の和はつねに等しい。
3. 定滑車で糸を引き上げる『きょり』とおもりが移動する『きょり』が等しい。
4. 定滑車で糸を引く『ちから』おもりのおもさは等しい。
5. 動滑車で糸を引き上げる『きょり』は、おもりが移動する『きょり』の 2倍。
6. 動滑車はおもりの 半分(1/2)の『ちから』で糸をひくことができる。
これらを覚えて、組み合わせ滑車などの応用問題に挑戦しましょう。

コメント