まず、多角形の内角の和を計算する簡単な公式がこれです。
n角形の内角の和 = 180 × (n – 2)
この多角形の内角の和についてなるべくシンプル簡単に紹介していきます。
基本的な図形の内角の和は皆さん知っていると思います。
(三角形の内角の和) = 180°
(四角形の内角の和) = 360°
ここまでは大抵の人が知っていると思いますが、六角形や八角形などを覚えている人は少ないかもしれません。
そこで今日は 簡単に覚えられる多角形の内角の和を紹介していこうと思います。
とても簡単なので、3分ぐらいで覚えることを目標にしましょう。
まずはじめに、内角の和の一覧表を紹介し、その後に簡単に計算できる公式を紹介していきます。
多角形の内角の和一覧表
| 多角形 | 内角の和 |
|---|---|
| 3角形 | 180° |
| 4角形 | 360° |
| 5角形 | 540° |
| 6角形 | 720° |
| 7角形 | 900° |
| 8角形 | 1080° |
| 9角形 | 1260° |
| 10角形 | 1440° |
| 11角形 | 1620° |
| 12角形 | 1800° |
5角形までの内角の和は覚えておいたほうがいいでしょう。
《多角形の内角の和》の簡単公式
まずは下の図形をみて下さい。
これらは三角形を基本として作られています。
どういうことかというと

下の図のように、点と点をつなぐことで複数の三角形が現れます。
するとどうなるでしょう。
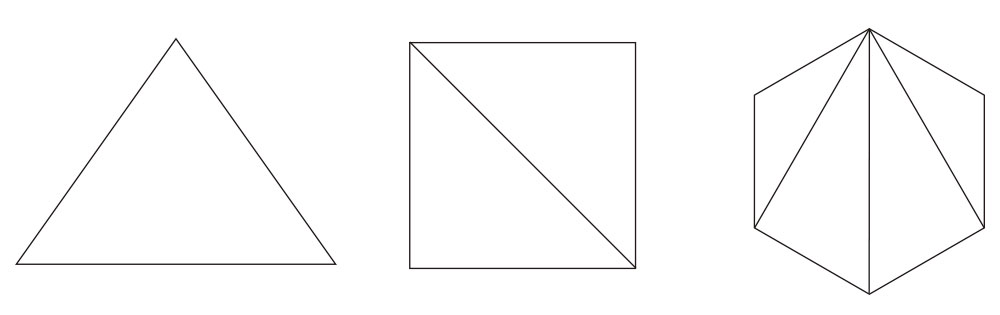
下の図をみて下さい。
三角形の内角の和は180°なので、現れた三角形の数に180をかけてやることで、
内角の和を求めることができるのです。
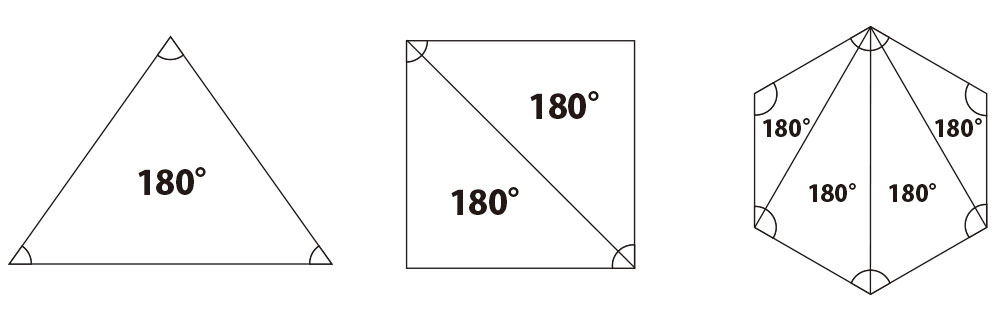
以上のことから、多角形の内角の和は下の公式で求められます。
多角形の内角の和 = 線を引いて現れた三角形の数 × 180
これをもっと簡単な公式にします。

上の図をると、三角形の数は多角形の角の数より2つ少ないことがわかります。
これを簡単な公式にすると
○角形の内角の和 = 180 × (○ – 2)
となります。 ○は角の数のことです。
例えば6角形の内角の和は
180 × (6 – 2) = 720
と求めることができるようになります。
内角の和は五角形ぐらいまでは暗記しておいたほうが時間の短縮になっていいのではないでしょうか。
それ以上は公式を使うのがおすすめです。
この公式についてですが
多角形の角の数をアルファベットの『n』に置き換えるのがいいと思います。
上記では角の数を『○』に置き換えていましたが、『n』は、これから高校や大学でも使用する『ある数』という意味です。
今から慣れておくのがオススメです。
つまり 多角形の和を求める簡単な公式は
n角形の内角の和 = 180 × (n – 2)
ということになります。
とても簡単なので、しっかり覚えて下さい!

コメント